A term that sparks curiosity and draws attention. In this article, we will embark on a journey to explore the world of diagonaux, a concept that finds its home in the realm of mathematics. Prepare to be intrigued and enlightened as we delve into the mysteries and applications of It.
Defining Diagonaux
Unraveling the Terminology
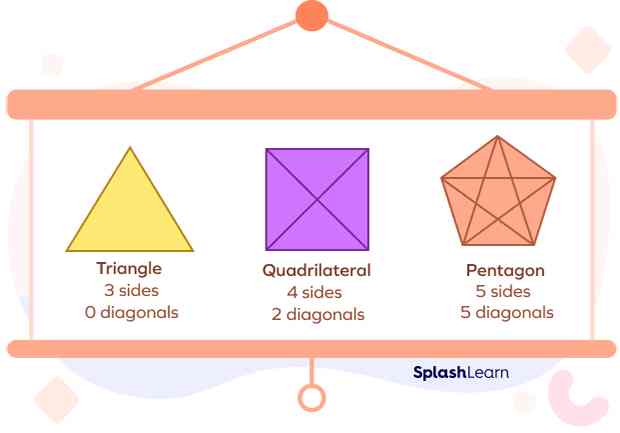
It mathematical terms, is a concept related to diagonals. Diagonals are straight lines that connect two non-adjacent corners or vertices of a polygon. Diagonaux, on the other hand, pertains to the properties, calculations, and applications associated with these diagonal lines.
The Wonders of Diagonals
Diagonals are not just lines; they are the backbone of geometry, connecting crucial points within various shapes, and serving as a foundation for numerous mathematical principles.
The Role of Diagonaux in Different Shapes
Triangles
In a triangle, diagonaux refer to the line segments that connect non-adjacent vertices. They have a significant role in understanding triangle properties, including area, angles, and congruence.
Rectangles and Squares
That in rectangles and squares create interesting relationships between sides and angles. They also split the shape into congruent right-angled triangles.
Polygons
For polygons with numerous sides, It help in understanding internal angles, creating triangles within the shape, and determining properties such as the sum of the interior angles.
Diagonaux and Circles
The Magical Circle
While circles may not have traditional diagonals, they have their own special lines and segments, such as diameters and radii. Understanding these concepts is crucial in geometry and trigonometry.
Secant Lines
Secant lines in circles can be considered as a type of Things, connecting two points on the circle’s circumference, and they have applications in trigonometric functions and calculus.
Diagonaux in Practical Applications
Architectural Design
It play a significant role in architectural design, helping architects create structures with specific angles, proportions, and aesthetic appeal.
Engineering and Construction
In engineering and construction, understanding the principles of It is essential for ensuring the stability and integrity of buildings and infrastructure.
Art and Design
Artists and designers use diagonal lines and concepts related to diagonaux to create dynamic and visually appealing compositions.
Pythagoras and the Diagonal
The Pythagorean Theorem
The Pythagorean Theorem is one of the most famous applications of diagonaux. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
The Role of Diagonaux
the context of the Pythagorean Theorem help establish relationships between the sides of right-angled triangles and enable calculations of lengths, areas, and angles.
Advanced Concepts in Diagonaux
Vector Mathematics
In vector mathematics, diagonaux are crucial for understanding vector addition and manipulation, helping in various applications in physics and engineering.
Diagonaux in Higher Dimensions
That extend into higher dimensions, where they connect non-adjacent vertices in polyhedra, providing insight into spatial geometry.
Analytical Geometry
Analytical geometry uses coordinates and equations to study geometric concepts, including diagonaux, in a more abstract and algebraic manner.
The Intriguing World of Fractals
Diagonaux and Fractal Geometry
Fractals are complex geometric shapes with self-replicating patterns. Diagonaux within fractals add a new layer of complexity to their study and understanding.
Recursive Diagonaux
In fractals, recursive It can be used to determine the length and properties of diagonal lines as they iterate through different scales of the fractal.
Conclusion
the mathematical concept of diagonals and their properties, are a fundamental element of geometry and mathematics. They play a vital role in understanding shapes, angles, and relationships in various mathematical disciplines. From the Pythagorean Theorem to architectural design, It have a wide range of applications in our daily lives. As we continue to explore the intriguing world of mathematics, we find that diagonaux are an essential and captivating aspect of this boundless realm.